Partiamo con qualche frase emblematica, giusto per fare un breve punto della situazione...
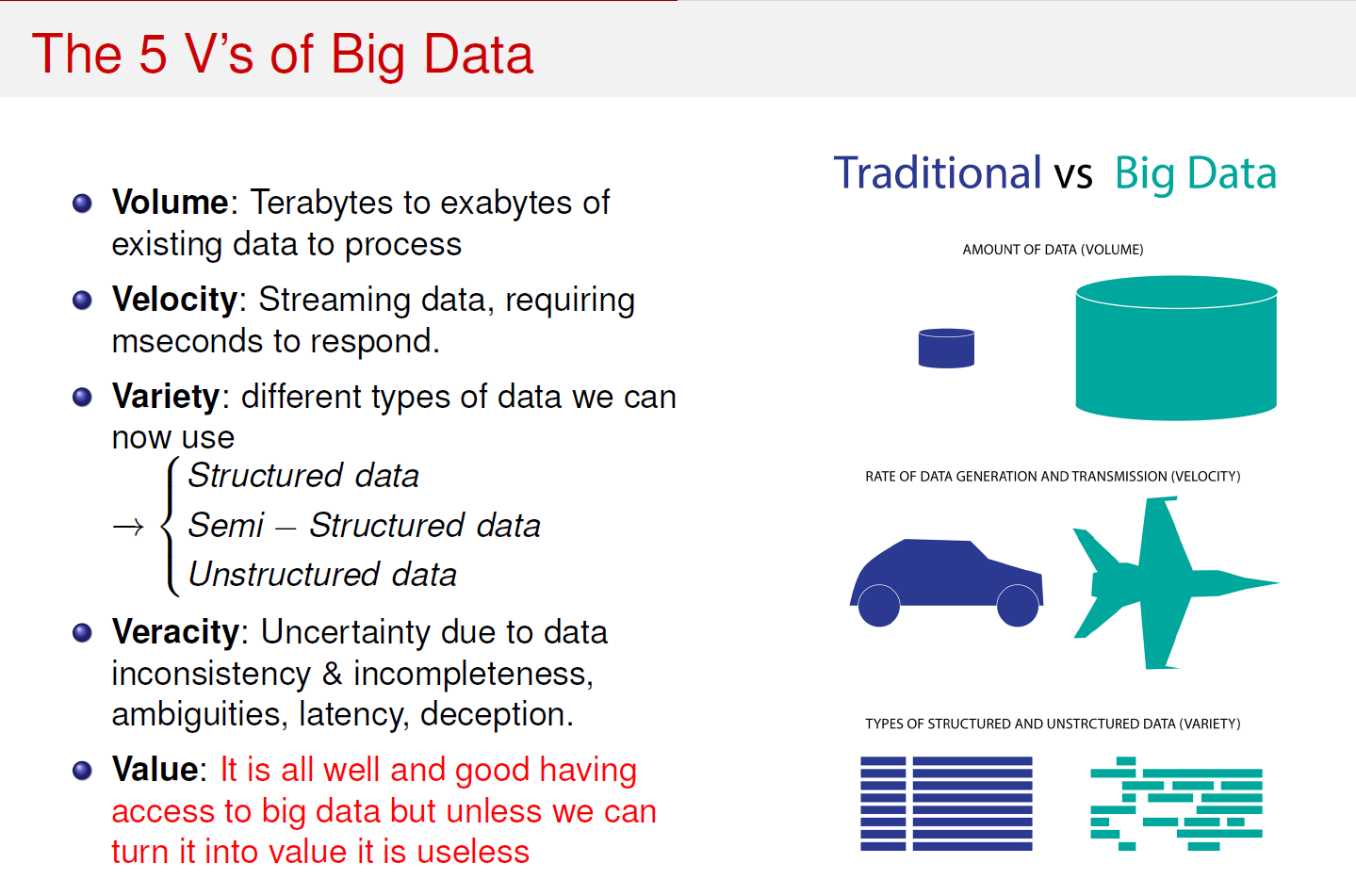
- "Si sta prospettando all'umanità una nuova rivoluzione socio-economica, paragonabile alla seconda rivoluzione industriale. Stiamo assistendo alla nascita dell'era dei Big Data."
- "I Big data sono il nuovo microscopio che rende “misurabile” la società."
- "Tutti dati che abbiamo acquisito negli ultimi 2 anni sono più di tutte le informazioni ricevute negli ultimi tremila anni."
- "Questo enorme volume di dati ha creato un nuovo paradigma di data processing chiamato Big Data Analytics, il quale costituisce una delle top ten strategic technologies."
Senza entrare troppo nel particolare...vediamo giusto qualche esempio.

Il problema della Big Data Analytics quindi deve essere affrontato su due fronti:
Algoritmi e modelli:
- Rappresentazione dei dati
- Riduzione della dimensionalità
- Calcolo parallelo
- Combinazione di modelli
Hardware e tecnologie:
- HPC (High Performance Computing)
- Cloud Computing
- Storage dei dati
- Scambio di dati
Un secondo esempio interessante al proposito...
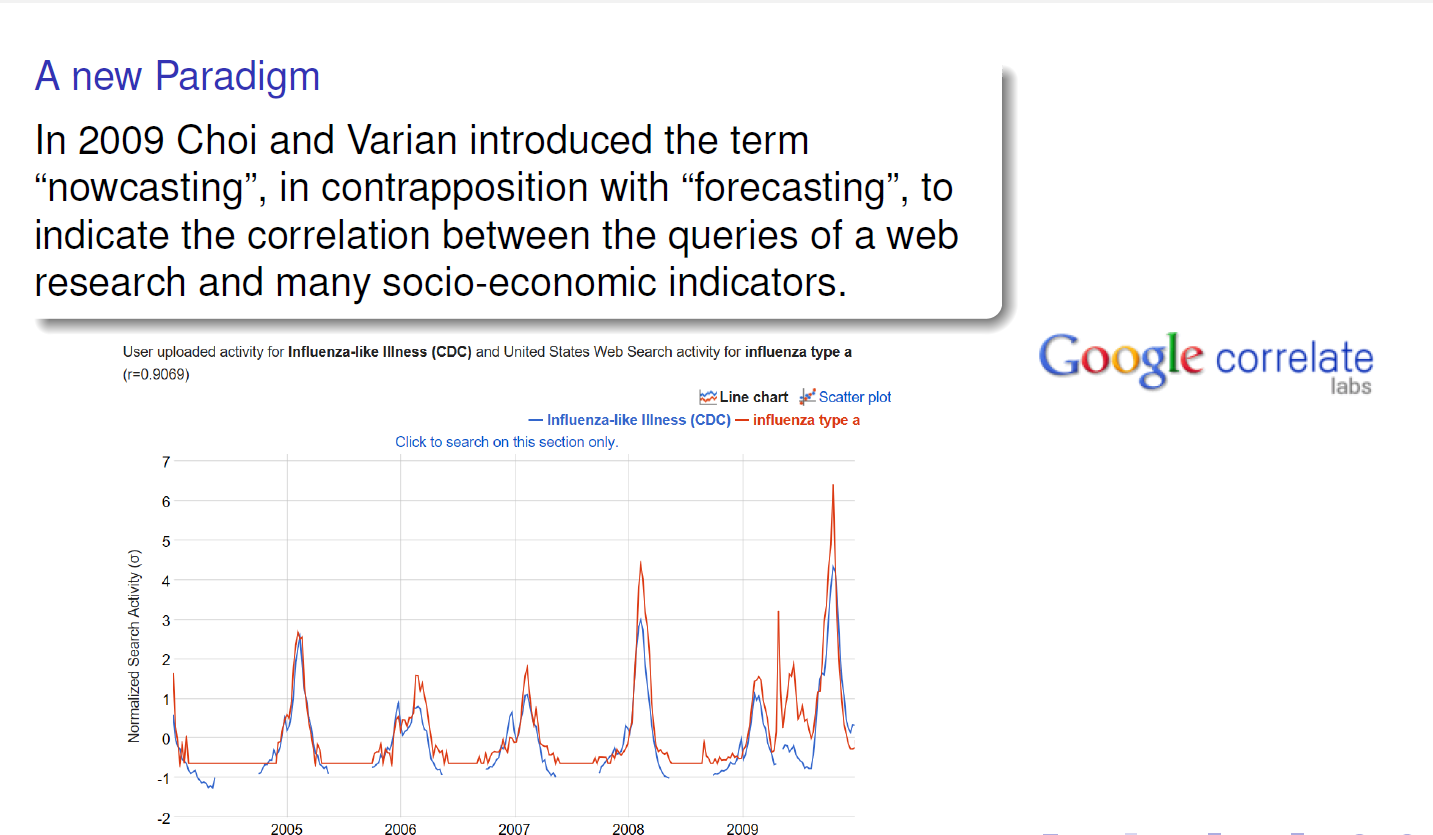
Rimaniamo su Google...che come al solito ne sà una più del diavolo!
Una delle "innovazioni" più importanti nell'ambito della Big Data Analytics è stato il cosiddetto paradigma MapReduce.
Paradigma Map Reduce¶
Con il termine MapReduce si intende una tecnica di programmazione per l'analisi di data set più ampi della capacità di memoria a disposizione.
Il framework software è stato brevettato da Google e attualmente vi sono implementazioni più o meno ottimizzate per la maggior parte dei linguaggi di programmazione.
Come funziona¶
Il framework è ispirato alle funzioni map e reduce utilizzate abbondantemente nella programmazione funzionale (queste funzioni sono presenti anche in Python come funzioni del linguaggio base!). Banalmente avremo:
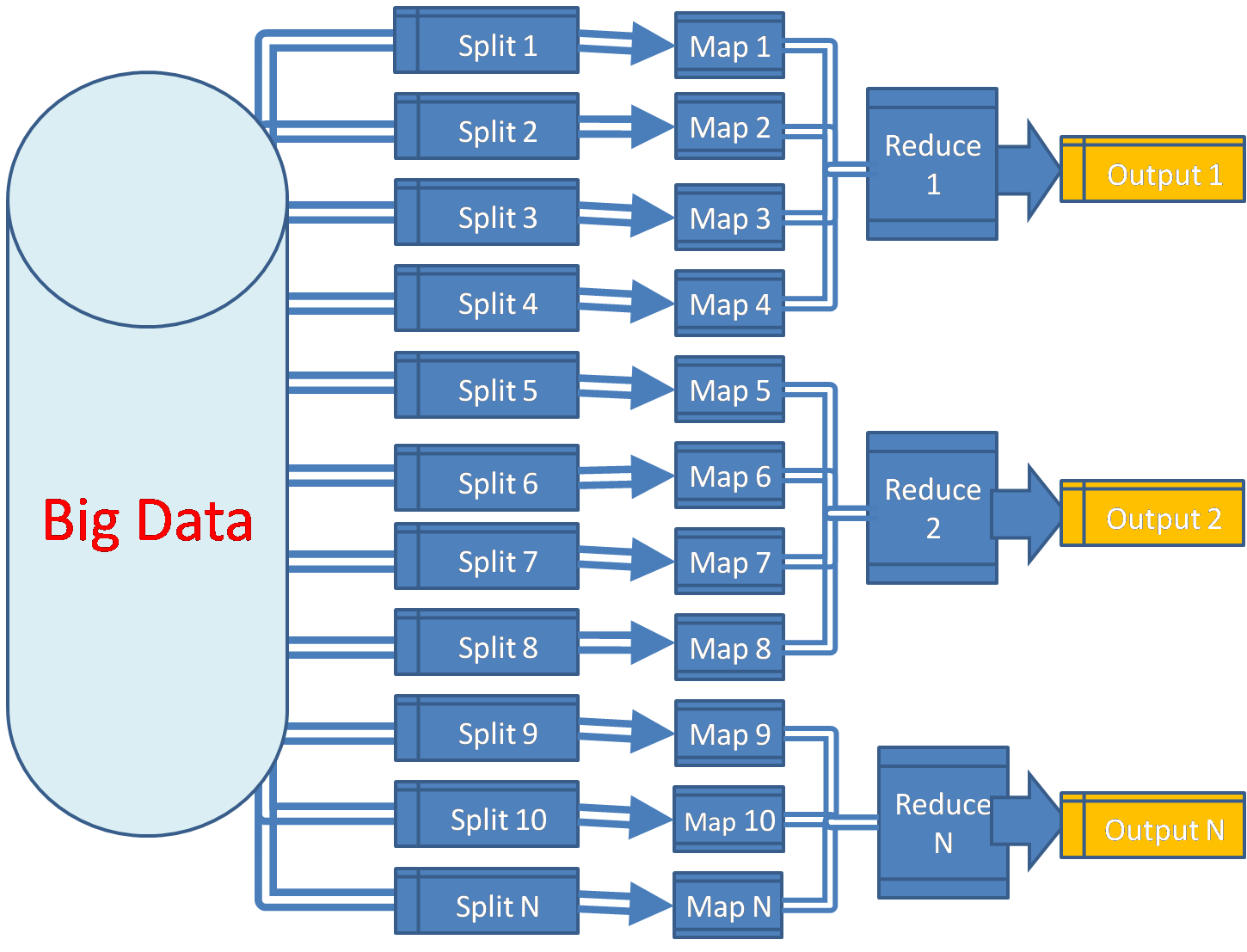
- MAP procedure: un nodo "master" prende i dati in ingresso, li suddivide in piccoli sotto-problemi e distribuisce il lavoro ai nodi "slaves".
- REDUCE procedure: il nodo "master" colleziona le risposte dei vari "slaves" e le combina nell'output finale.
# Calcolo del numero totale di elementi presenti
# in una serie di liste
a = [1,2,3] # lista1
b = [4,5,6,7] # lista2
c = [8,9,1,2,3] # lista3
L = map(lambda x:len(x), [a,b,c]) # map su tutte le liste (calcolo len di ognuna)
# L == [3,4,5]
N = reduce(lambda x, y: x + y, L) # sommo tutte le len
print("L = %s\nN = %s"%(L,N))
L = [3, 4, 5] N = 12
Niente di nuovo...o quasi¶
Se vi ricordate la lezione riguardo la vettorizzazione questo processo di MAPPING dovrebbe suonarvi familiare!
- Applicare una funzione su tutti gli elementi di un vettore indipendentemente.
- Riassumere il risultato delle operazioni in un altro oggetto.
def quadrato(n):
return n**2
numeri = [0,1,2,3,4,5,6]
quadrati = map(quadrato, numeri)
print(quadrati)
[0, 1, 4, 9, 16, 25, 36]
In modo analogo il processo di REDUCTION permetterà di combinare insieme i risultati di un'iterazione come se facessimo un ciclo.
def somma(a, b):
return a+b
totale = reduce(somma, numeri, 0)
print(totale)
21
Il metodo MapReduce è una combinazione di queste idee:
prendo una sequenza, la divido in sottosequenze
invio le sequenze a diversi computer
compio una riduzione su ciascuna sotto-sequenza
raccolgo le sotto-sequenze e le combino insieme
Tutto questo fatto in modo ricorsivo.
Riassumendo...¶
- Molto utile quando si hanno a disposizione algoritmi per il calcolo parallelo e/o distribuito.
- La condizione di applicabilità è legata alla scomposizione del problema iniziale in sotto-problemi.
- In genere i sotto-problemi sono tutti uguali.
NOTA: sotto-problemi uguali e semplici permettono implementazioni altamente parallelizzate e non solo su CPU ma anche su GPU (Heterogeneous Computing).
Vediamone un esempio applicativo più articolato¶
Vediamo come possiamo impostare un codice che operi mediante MapReduce per l'analisi di un piccolo Big Data!
Oggi cambiamo un po'...e vediamo qualcosa in Matlab!
NOTA: Quanto visto fin'ora nelle lezioni precedenti vi dovrebbe essere sufficiente per riuscire a "tradurre" la lezione di oggi anche in Python!
Codice MapReduce.m¶
Arrays in Big Data problems¶
Di norma quando pensiamo a dati immaginiamo di vederli disposti in array anche a svariate dimensioni.
Tuttavia quello che capita spesso è che:
I dati (magari quelli più importanti) siano solamente pochi rispetto al totale;
Ci siano numerosi dati mancanti
Quindi possiamo affermare, senza ledere troppo la generalità, che spesso è volentieri i dati siano sparsi.
Un tipico/banale esempio lo troviamo nei modelli a network, in cui rappresentiamo un grafo mediante una matrice di adiacenza che conterrà un numero specifico di valori numerici identificativi dei link, "immersi" in un mare di valori nulli.
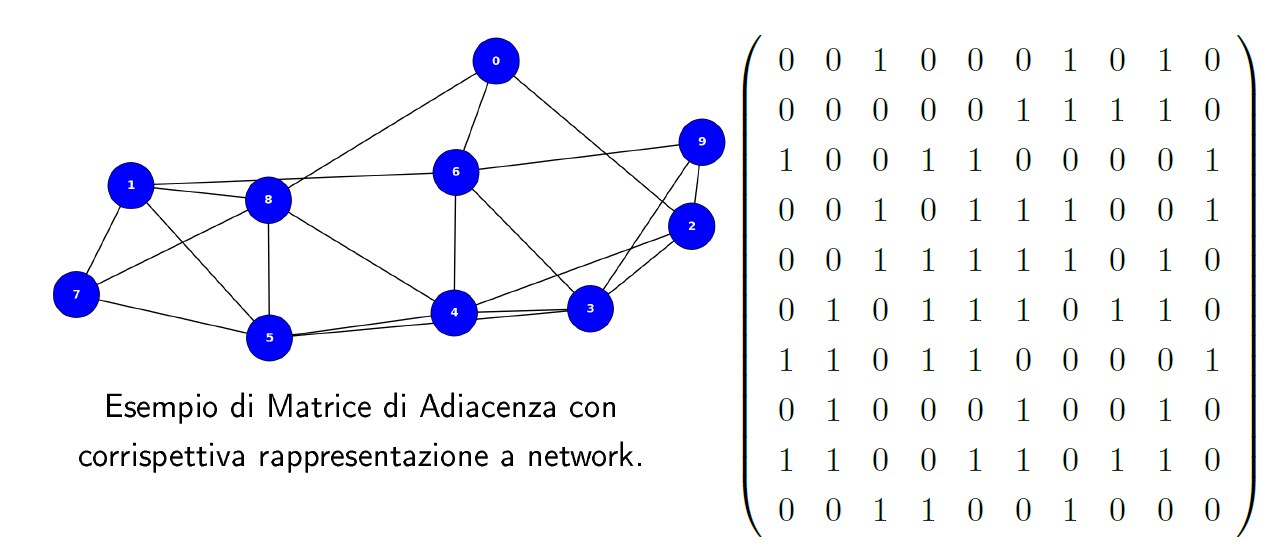
Quello che sorge spontaneo chiedersi a questo punto è:
Tutti quegli zeri ci servono davvero?!
L'informazione dopotutto è contenuta nei valori non nulli!E ancora:
Sarebbe un peccato sprecare memoria e calcoli per valori che
non ci interessano!Questo è proprio uno dei punti di maggior sviluppo della moderna algoritmica, ovvero l'algebra sparsa.
NOTA: una piccola nota per rigore matematico. Ci sono diverse definizioni di sparsità che comportano diverse proprietà e diverse tipologie di ottimizzazione. Grossolanamente possiamo dire che una matrice $N\times N$ è "sparsa" qualora possieda solamente un numero di valori non nulli $\sim O(N)$.
Codice SparseMat.m¶
Riassumendo:
Non sempre considerare matrici sparse è efficiente
Bisogna sempre considerare la complessità algoritmica!
NOTA : la complessità algoritmica delle operazioni sparse è proporzionale ad nnz (number of non-zero elements).
Remember, remember (law):
"Premature optimization is the root of all evil" (cit. Donald Knuth)
o anche...
"Da un grande potere derivano grandi responsabilità" (cit. zio Ben)Alcune (di una lunghissima serie..) regole fondamentali per la programmazione di algoritmi ad alte performance sono:
- Considerare sempre la complessità algoritmica del proprio codice e trovare la soluzione migliore per ogni caso che si intenda valutare.
- Tenere a mente che la generalità di un algoritmo è inversamente proporzionale (in genere) alla sua efficienza (più qualcosa è specifico per un problema e maggiormente è ottimizzabile il problema stesso).
- Prima di procedere all'ottimizzazione occore sapere BENE quali siano i punti più dispendiosi (in termini di tempi di calcolo) del nostro codice (Profiling).
Data representation¶
Un altro topic principale per l'ambito dei Big Data è la rappresentazione dei dati e dell'informazione estraibile da questi dati.
Ovviamente parlando di Big Data stiamo considerando dati ad elevatissima dimensionalità ($\gg 3$, dimensione "massima" per un plot).
Ciò che occorre fare allora è riuscire ad estrarre l'informazione di maggior rilevanza presente nei dati e "sperare" che questa abbia una dimensionalità inferiore rispetto a quella iniziale.
Una delle tecniche base per farlo (o comunque da utilizzare praticamente sempre come primo step per vedere i dati) è l'Analisi delle Componenti Principali (PCA).
NOTA: la PCA è un metodo di riduzione della dimensionalità basato sulla proiezione dei dati lungo le direzioni di maggior varianza di questi. In questo modo vengono contemplate solamente le direzioni di maggior dispersione dei dati e resi visivamente distinti, o almeno quello è ciò che si spera.
Vediamo un esempio di come poter fare ad utilizzare questa tecnica in Matlab...
Codice PCA.m¶
Ora tocca a voi¶
Il compito di oggi è quello di scrivere una versione ottimizzata dell'algoritmo di PCA, denominato, per l'appunto, FastPCA. Per testare il vostro codice potete utilizzare sempre il FisherIris.
Come spesso vi accadrà quando cercherete un codice...l'unica cosa che avete a disposizione è lo PseudoCode:

Inoltre...per chi è proprio bravo bravo!
Creare un grafico con le prime due componenti principali a scatter plot.
E due plot affiancati delle proiezioni dei dati lungo i due assi.